线性回归

1.例子

举个例子：

给定这样的X、Y值：(1,1)、(2,2)、(3,3)、(4,4)、(10,10)，问当X=5时，Y等于多少？显然Y=5；建立了X与Y的关系：$Y=X$

再看一个难一点的例子：给定这样的X、Y值：(1,1)、(2,4)s、(4,16）、(100,10000)，问当X=5时，Y等于多少？显然Y=25，同样建立了X与Y之间的关系：$Y=X^2$

再举个例子：

• 期末考试成绩=0.7 考试成绩+0.3 平时成绩 ----------- 建立这样的一个关系：$Y=0.7*x_1+0.3*x_2$

  （$x_1$代表考试成绩、$x_2$代表平时成绩、$Y$表示期末成绩）

• 房子价格=0.02 中心区域的距离 + 0.04 城市一氧化氮浓度 +0.2 * 城镇犯罪率---------建立关系：$Y=0.02*x_1+0.04*x_2+0.2*x_3$（其中Y为房价、$x_1$为中心区域距离、$x_2$为城市一氧化氮浓度、$x_3$为城市犯罪率）

线性回归就是采用这样的工作原理。计算机会通过"理解"给定的数据，尝试确定X和Y之间”最合适“的关系。使用建立好的关系就可以预测给定的X值并预测未知的Y值（X记为特征值、Y记为目标值，建立特征值与目标值之间的关系---->回归方程）

特征与目标之间关系画图分析

特征值：房屋面积（单特征值）

目标值：房屋价格

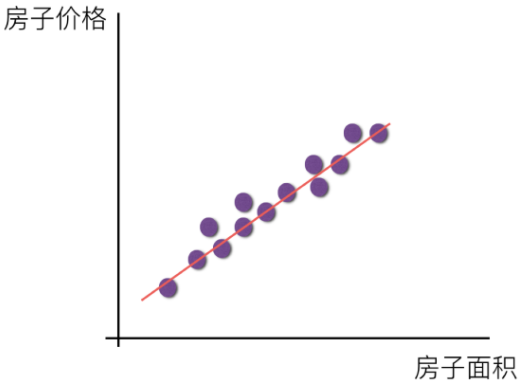
特征值：$X_{1}代表面积,X_{2}代表朝向$

目标值：$Y代表房屋价格$

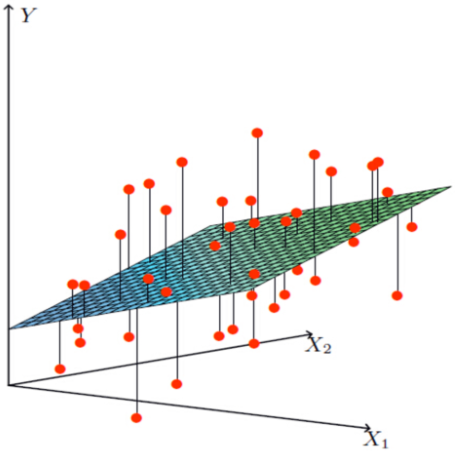
红点代表的就是实际的目标值（房屋价格）；平面上和红点竖向相交的点代表我们根据线性回归模型得到的点。也就是说实际房屋价格和预测的房屋价格是有一定差距的，这个就是误差项。

2.符号约定与定义

​ 线性回归(Liner regression)是利用回归方程(函数)对一个或者多个自变量（特征值）和因变量（目标值）之间的关系进行建模的一种分析方式。

(1)符号约定

• $X^{(i)}$代表一个样本（一行就是一个样本）
• $X_{i}$代表一个特征值
• $Y$代表目标值

(2)假设函数

$\begin{aligned} h_{θ}(x)&= θ_{1}x_{1}+θ_{2}x_{2}+θ_{3}x_{3}+...+θ_{n}x_{n}+b\\ &=θ_{1}x_{1}+θ_{2}x_{2}+θ_{3}x_{3}+...+θ_{n}x_{n}+θ_0x_0(其中x_0=1,θ_{0}=b)\\ &=\sum_\limits{i=0}^{n} {θ_ix_i}\\ &=θ^{T}X\\ \end{aligned}$

$其中θ,X可以理解为矩阵:θ= \left\{ \begin{matrix} θ_{0} \\ θ_{1} \\ \vdots \\ θ_{n} \end{matrix} \right\} , X= \left\{ \begin{matrix} 1 \\ x_{1} \\ \vdots \\ x_{n} \end{matrix} \right\}$

(3)损失函数

总损失定义如下： $\begin{aligned} L_{θ}(x)&= (h_θ(x_1)-y_1)^2+(h_θ(x_2)-y_2)^2+(h_θ(x_3)-y_3)^2+...+(h_θ(x_n)-y_n)^2\\ &=\sum_\limits{i=1}^{n} {(h_θ(x_{i})-y_{i})^2}\\ \end{aligned}$

• $y_i$为第i个训练样本的真实值
• $h_θ(x_i)$为第i个训练样本特征值组合预测值
• 又称为最小二乘法

为了使我们预测的更加准确，如何减小这个损失？我们一直说机器学习有自动学习的功能，在线性回归这里更是能够体现。这里可以通过一些优化方法去优化（其实就是数学当中的求导功能）回归的总损失！

3.求解使得损失最小对应θ的方法

求解θ目的：寻找模型中的θ，使得损失（误差项）最小（更好拟合）

(1)正规方程求解θ矩阵推导

一步可以求解θ矩阵使得损失最小：$θ=(X^{T}X)^{-1}X^{T}Y$

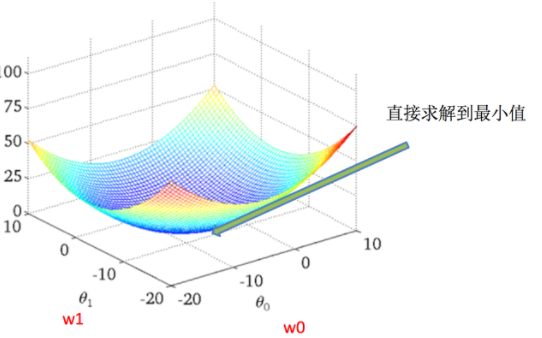
X为特征值矩阵；Y为目标值矩阵，直接求到最好的结果

缺点：当特征过多过于复杂时，求解速度太慢并且得不到结果

正规方程推导过程：

$Y^{(i)}=h_θ(x^{(i)})+ε^{i}$

解释：

• $Y^{(i)}代表第i个样本对应的真实值$
• $h_θ(x^{(i)})代表第i个样本对应的预测值$
• $ε^{i}代表第i个样本对应的误差项：误差ε^{(i)}是独立同分布，且服从均值为0方差为θ^2的高斯分布$
  • 我们根据实际情况，假设认为这个误差项是满足以下几个条件
    • （1）独立：任意样本之间互不影响，不同房屋之间互不影响 P(AB)=P(A)P(B)独立，说明AB独立
    • （2）同分布：服从高斯分布

开始推导：

(2)梯度下降法

4.特征归一化

5.欠拟合与过拟合

6.Ridage回归

7.LASSO回归

8.房价预测案例